What is Topology Optimization? A Guide to Efficient Design Techniques

Topology optimization software is applied across various engineering fields, from structural engineering to fluid dynamics. Topology optimization is a mathematical method for improving material distribution within a given space. The article will show how it is used during the design process to achieve optimal designs.

Topology optimization is a method that optimizes a geometry layout within a given 3D design space following a defined set of rules. The term itself reflects its purpose: derived from the Greek "tópos" (place or domain) and "lógos" (reasoning) and Latin "optimum" (the best), topology optimization seeks the best material arrangement within a defined domain. 

Engineers use topology optimization software to refine structures. At the same time, they can impose manufacturing processes and constraints.

Engineers using topology optimization software can predict performance and identify design flaws well before production. This approach is particularly valuable when lightweight, high-performance components are essential.

Examples of improvements over traditional manufacturing methods are in the aerospace, automotive, and medical industries.

What is Topology Optimization?

Topology optimization is a computational technique determining the optimal material distribution and shape within a predefined design space. The goal is to optimize an object's design, i.e., to maximize its performance criteria, such as strength or stiffness.

However, within a realistic design optimization, we cannot push for engineering performance "whatever it takes." We need to minimize parameters such as used material or cost. The topology optimization process deals with shape optimization so that the geometry will realistically meet performance objectives.

The topology optimization method is mainly used in the aerospace and automotive industries to design lightweight yet structurally efficient components. Removing unnecessary material while maintaining strength reduces weight and yields better fuel efficiency.

This approach is particularly valuable in aircraft structures, engine components, and chassis design, where minimizing mass without compromising safety is critical.

Topology optimization is also used in civil engineering to develop innovative and sustainable building systems. Architects and engineers use this method to design bridges, high-rise buildings, and infrastructure components that balance durability, aesthetics, and environmental sustainability.

Topology and Topology Optimization

Topology is a branch of mathematics that deals with the properties of spaces that are preserved under continuous deformations, e.g., stretching, twisting, or bending, without tearing or gluing. The central idea in topology is to focus on the qualitative properties of shapes and objects rather than precise measurements or distances.

Topological optimization methods use concepts from topology, particularly continuous deformation, where the “shape” of a structure is modified during the optimization (without cutting, creating holes, etc.).

The outcome provided by topology optimisation software often resembles organic shapes suitable for 3D printing, which aim to minimize material without compromising structural strength.

Key Principles of Topology Optimization

The four key ingredients of topology optimization are:

The Design Space is the volume where the material can be distributed, defined by the engineers. It represents the allowable volume in which the topology optimization algorithm searches for the best material layout. Engineers define the initial design space based on functional, geometric, and manufacturing constraints. The final structure after material removal is a lightweight and efficient geometry.

Objective Function. The optimization goal could be to minimize weight, maximize stiffness, improve thermal conductivity, or achieve a specific load distribution. The objective is defined mathematically and forms the basis of the optimization process.

Material Distribution. Topology optimisation finds the optimal layout for material within the design space, essentially determining where the material should be placed and where it should be removed to meet the performance criteria.

Constraints include limits on the design's material usage, stress, displacement, temperature, and other parameters related to manufacturability. These parameters ensure that the optimized design meets practical requirements and that shape optimization does not lead to theoretical solutions that are not cost-effective enough to be produced.

For instance, for a certain product, one could set the constraint that all holes must be at least 2 mm in diameter or that no internal features can have walls thinner than 1 mm to account for manufacturing restrictions, making the production costs more affordable. In practice, once topological optimization generates an initial design, this design could be  exported to CAD software for further refinement. Here, design tools for manufacturability (DFM) are used.

Application Beyond Structural Design

While traditionally associated with structural integrity - such as creating lightweight, robust components- topology optimization can be applied to various engineering challenges.

In structural optimization, mechanical or civil engineering designs are concerned with load-bearing structures that minimize material usage while maintaining strength and stability, such as designing lighter yet stronger beams or frames.

In Fluid Dynamics, topology optimization extends to fluid flows in applications such as aerospace or automotive industries. It helps design the optimal shape of air ducts, turbine blades, or heat exchangers.

Key Benefits of Topology Optimization

Topology optimization allows the creation of innovative shapes that would not be conceived through traditional methods.

Topology optimization helps reduce weight and material waste by removing unnecessary material, leading to cost savings and improved environmental sustainability.

How Does Topology Optimization Work?

Topology optimization formulates an objective function that defines a structure's performance goals. An example is maximizing stiffness while minimizing weight.

The finite element method is one of the most common techniques used for topology optimization to analyze and finalize designs. FEM / FEA is employed to evaluate how the design responds to various loading conditions. Optimization involves adjusting the design space's element density field, removing redundant material, and refining the layout to achieve optimal results.

This image represents a topology optimization process for a mechanical part. The goal is to minimize material usage while maintaining structural integrity under boundary conditions. The final design is smoothed and prepared for various manufacturing processes, such as additive manufacturing (3D printing).

Design Space and Constraints

The design space is the allowable volume in which material can be placed. This is a 3D domain representing defined geometric boundaries (e.g., a rectangular block for a bracket), manufacturing constraints, such as minimum feature size or symmetry requirements, and forbidden regions where material cannot be added.

Optimization Algorithms

Topology optimization algorithms differ based on the problem type and computational resources. The SIMP method is popular for its simplicity in structural optimization. Each method enhances engineering solutions in areas like structures and fluid dynamics.

Solid Isotropic Material with Penalization (SIMP) - Mathematical Method

SIMP is widely employed in topology optimization, especially in structural applications. It utilizes a “material density” ρ=ρ(x) function to represent the material distribution within any point x of the design space.

The design is defined by ρ that ranges from 0 (no material) to 1 (all solid material), establishing the distribution throughout the domain.

SIMP incorporates a penalization function to discourage "intermediate" material states (e.g., ρ=0.5) and forces the solution toward either solid (ρ=1) or void (ρ=0). The Objective in SIMP typically involves the minimization of structural compliance (which relates to maximizing stiffness) subject to various material properties and constraints:

• Minimize structural compliance: C = ∫ σ(x)⋅u(x) dV where σ is the stress, and u is the displacement.
• Material volume constraint: ∫ ρ(x) dV = V_target on the target material volume.

Optimization iteratively adjusts the density values across the design domain until an optimal material layout is found.

Example

• V_target: If you’re designing a lightweight bridge, you might have a budgeted amount of material V_target (e.g., 55% of the entire design space). The optimizer removes material in low-stress areas while it keeps enough material in high-stress regions to maintain structural integrity.
• C: Combined with the compliance minimization equation, this ensures the stiffest possible bridge using the least amount of material. If you’re designing a lightweight bridge, you want to distribute the material so that it resists deformation efficiently while using the least amount of material. By minimizing C, the optimization algorithm removes inefficient material while strengthening the structure.

Heuristic Methods in Topology Optimisation

SIMP is a gradient-based method. It relies on numerical gradients of the objective function (e.g., compliance, stiffness, weight) to iteratively refine the material distribution within a design space.

Heuristic methods are helpful, particularly with highly nonlinear objectives or conflicting constraints (e.g., weight vs. stiffness vs. manufacturability). These topology optimization techniques explore a broader space without depending on gradients and can avoid local minima.

Heuristic methods include:

• GA (Genetic Algorithms) is a mathematical method inspired by natural selection that evolves designs using selection, crossover, and mutation.
• Simulated Annealing is a probabilistic optimization algorithm inspired by the physical annealing process. This analogy is used to find a global optimum by simulating the gradual cooling process.
• In Particle Swarm Optimization, design candidates move through the search space, influenced by their own and neighbors' experiences.

Overall, those methods excel in complex geometries and multi-disciplinary optimization goals.

Finite Element Analysis (FEA)

FEA's role in topology optimization is to assess the structural performance of designs throughout the iterative process. As a first step, we define the design space, including boundary conditions, applied loads, and material properties. The initial geometry is meshed into finite elements, allowing the solver to calculate stress distribution, strain, and displacements under the given conditions.

The optimization algorithm removes material that contributes minimally to structural integrity while preserving load paths. A new FEA simulation is performed at each iteration to validate performance and refine the design. This process continues until an optimal configuration meets criteria such as weight reduction or improved stiffness-to-weight ratio.

Benefits of Topology Optimization

As a reminder, topology optimization is a computational approach that optimizes material distribution within a given design space to achieve maximum performance while minimizing weight and material. Its primary applications are engineering fields such as aerospace, automotive, and industrial design, particularly in combination with additive manufacturing. Below are the key benefits.

Material Efficiency

Topology optimization removes unnecessary mass while maintaining structural integrity. This reduces raw material consumption, lowers production costs, and minimizes waste. The technique is particularly beneficial when using high-performance materials (e.g., titanium or composites), where reducing material usage impacts overall expenses.

Furthermore, with additive manufacturing, topology optimization unlocks complex, "organic" structures that would be impossible to produce with traditional subtractive methods. This synergy between optimization and additive manufacturing maximizes material efficiency and lightweight strategies.

Performance Improvement

Optimized structures use less material and achieve higher stiffness-to-weight ratios, improved load distribution, and enhanced fatigue resistance. Topology optimization reduces stress concentrations by directing material where it is needed.

Innovative Design Solutions

Engineers can create non-intuitive, highly optimized forms by implementing topology optimization early in the design phase. Instead of relying on conventional shapes, the algorithm explores the design space in ways that may not be immediately obvious to human designers.

This approach benefits industries like aerospace or motorsport (see figure), where maximizing performance per weight is essential for fuel reduction in conjunction with optimizing external aerodynamics performance. Topology-optimized designs often incorporate biomimicry, resulting in organic, lattice-like structures that mimic natural load-bearing geometries.

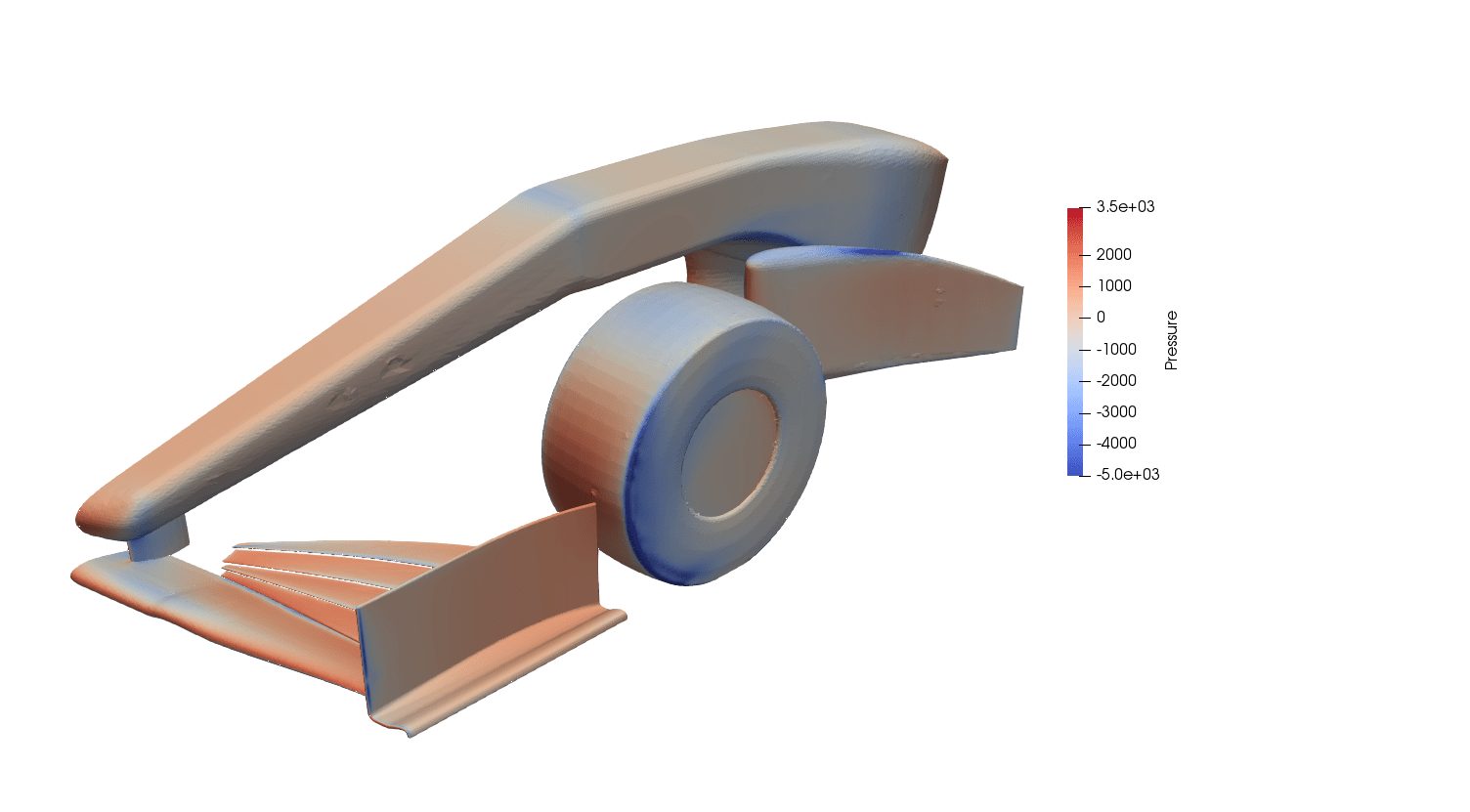
Common Applications

In this section, we will show topology optimization enabling the creation and mass production of lightweight, high-performance structures in various industries.

Aerospace Engineering

By integrating topology optimization with additive manufacturing, aerospace engineers can produce high-performance structures that would be impossible to manufacture using traditional methods.

Topology optimization helps design lightweight yet strong aircraft components and in turbomachinery and thermodynamics optimization, such as:

• Structural brackets that withstand extreme loads while minimizing mass.
• Landing gear components optimized for durability and reduction of weight.
• Engine mounts and internal airframe structures that balance strength and manufacturability.

Automotive Industry

Topology optimization is commonly used at the design stage of new products to optimize the form and increase the stiffness-to-weight ratio.

Weight reduction enhances the performance of chassis components such as subframes and suspension arms. Electric vehicle battery enclosures are optimized for strength and thermal performance. Crash-resistant structures absorb impact forces while minimizing material.

Consumer Products

Topology optimization is used in consumer products to enhance performance and reduce material costs with lighter and stronger products.

• Bicycle frames, tennis rackets, and running shoe soles are optimized for weight reduction and durability.
• Topology optimization benefits ergonomic furniture, achieving minimal material usage while maintaining strength and comfort.
• Laptop casings, cooling systems, and internal support structures are optimized for heat dissipation, durability, and weight.

Challenges in Topology Optimisation

Topology optimization offers significant benefits, but its practical implementation comes with challenges.

Manufacturing Constraints and Additive Manufacturing

One major issue is manufacturing constraints. Optimized designs often feature complex geometries that are difficult or impossible to produce with traditional manufacturing methods like casting or machining. Additive manufacturing helps overcome this but still has material selection and production scale limitations.

Computational Resources

Another challenge is the high computational demand. Running topology optimization requires advanced finite element analysis (FEA) and iterative simulations, which need powerful computing resources and specialized software. This makes it costly and time-intensive, especially for large-scale industrial applications.

Validation and Testing

Finally, validation and testing are crucial to ensure optimized structures perform as expected. While simulations provide theoretical insights, real-world factors like material defects, load variations, and environmental conditions must be accounted for through rigorous prototyping and physical testing to guarantee reliability and safety in final applications.

Advanced Technologies Enhancing Topology Optimization

While topology optimization software solutions are pretty new, a newer technology known as Deep Learning (the most productive branch of AI) is on the market. How can it positively affect topology optimization? Check it out in the following two sections.

The Role of AI in Optimization

Traditionally, the Topology optimization process has been computationally demanding, requiring extensive simulations and iterative trials to reach an optimal design. However, artificial intelligence (AI), especially machine learning and 3D Deep Learning, has transformed topology optimization by enabling faster and more efficient solutions. AI can analyze large datasets, learn from previous design iterations, and generate optimized solutions with minimal human involvement, significantly accelerating the process.

Applications Across Industries

Neural Concept Shape exemplifies how AI, specifically neural networks, enhances topology optimization. Geometrical deep learning can deal with engineering prediction and shape optimization.

The platform can optimize intricate shapes based on performance criteria. Rather than relying on traditional simulations, the Neural Concept platform employs a data-driven method that identifies CAD model patterns, predicts their performance, and optimizes them, cutting down time and cost in the design process.

By training on extensive simulations or experimental results datasets, the neural network quickly learns essential physical behaviors associated with geometry features of complex structures within the specific engineering context. As an AI surrogate for FEA or CFD, it predicts (in almost real-time) the performance of new designs. This enables engineers to explore several design options in significantly less time than conventional methods.

The applications range from CFD and thermal (e.g., F1 car aerodynamics or heat exchangers) to electromagnetism, advanced FEA, crashworthiness and drop tests, and more. Industries include automotive, aerospace, biomedical, civil engineering, and electronics.

One of the most attractive benefits is that the platform can be adapted around the end user's needs for speed of response, lightweight IT usage, and ease of use as a design tool, either as a standalone app or within a CAD environment.

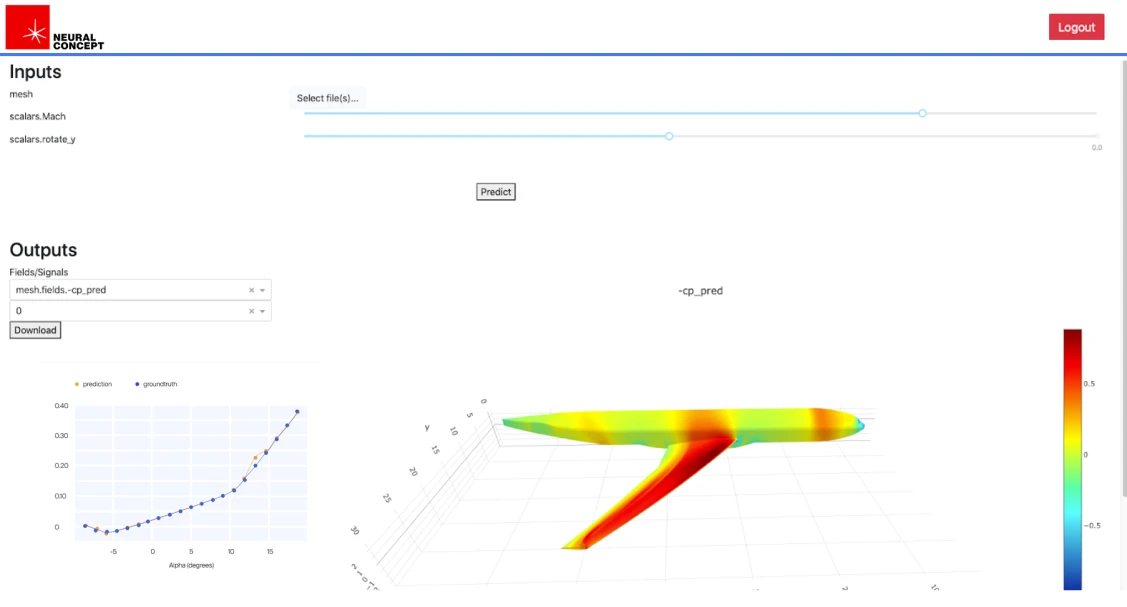
Conclusion

Topology optimization is essential in modern engineering to enhance structural design. It allows engineers to maximize performance by optimizing material distribution within a design space, balancing efficiency, strength, and cost. As industries pursue innovation, topology optimization becomes helpful for improving designs.

We showed how the Neural Concept platform is a design tool for tackling complex engineering problems in various applications and industries. The data-driven algorithms streamline the optimization process, exploring more design iterations while yielding faster results thanks to real-time response.

FAQ

What is the aim of topology optimization?

Topology optimization aims to find the optimal material distribution within a specified design space. This process enhances structural performance while minimizing weight and material usage, resulting in designs that meet specific performance criteria and constraints.

What is the objective function in topology optimization?

Objectives in topology optimization define the optimization process's goals, such as maximizing stiffness, minimizing weight, or optimizing energy efficiency.

How does topology optimization differ from generative design?

When discussing topology optimization vs. generative design, one should not forget that generative design includes topology optimization as a subset but is not limited to it. In topology optimization, engineers start with a shape and use software to find the best material layout, removing excess material. Generative design leverages AI and computational algorithms to generate and evaluate numerous design alternatives rather than starting from a single initial shape.

Can you give me examples of topology optimization software?

Altair OptiStruct is a tool for structural topology optimization. Autodesk Fusion 360 includes a cloud-based topology optimization tool accessible to engineers for design iterations in 3D modeling environments. Tosca by Dassault Systèmes is another solution for topology and shape optimization. These and other software tools are used in the automotive, aerospace, and energy sectors.

‍