Machine Learning Optimization: Best Techniques and Algorithms

Optimization is the process of finding the best solution from all possible choices. We seek to minimize or maximize a specific objective. In this article, we will clarify two distinct aspects of optimization—related but different. We will disambiguate machine learning optimization and optimization in engineering with machine learning.

• I. Optimization of Machine Learning refers to model optimization. "Optimization I" or Model optimization focuses on improving a machine learning model’s performance. The techniques used are hyperparameter tuning, feature selection, architecture design, and training refinement. Machine Learning experts handle these tasks using various tools. We will describe Bayesian optimization and gradient-based methods in detail. Experts rely on statistical learning theory and computational optimization techniques to enhance performance. Their experts' role is to refine models. They identify optimal architectures and optimize computational resources.
• II. Optimization with Machine Learning means using Machine Learning to optimize products and processes. The aim here is innovative product design. “Optimization II,” or Engineering Optimization, takes Machine Learning to every designer’s desk. Reliable predictive models are honed in “Optimization I”. Predictive models are coupled to consolidated optimization techniques we will describe.  Examples of optimization techniques are genetic algorithms. The approach uses pattern recognition and predictive capabilities of Machine Learning to identify optimal solutions in engineering or other fields (logistics, etc.).  In this approach, machine learning can even be “embedded". For instance, final users optimize projects using an App. Engineers can use it in manual searches in their design space. In a more advanced approach, they use algorithmic optimization.

What is Machine Learning-Based Optimization?

Machine Learning-based Optimization (or Optimization II, as in the introduction) leverages machine learning techniques to enhance product and process optimization across various engineering domains.

Traditional optimization methods often struggle in high-dimensional, non-convex, or computationally expensive design space. As dimensions increase, search spaces grow exponentially, making exhaustive exploration infeasible for the search of optimal hyperparameters. Also, many real-world problems have multiple local minima, where gradient-based methods can get stuck (non-convexity). A crucial point is that evaluating complex simulations (e.g., CFD, FEA) for every iteration is expensive and slow. Moreover, traditional methods don’t learn from past optimizations, while ML models can generalize and accelerate future searches.

ML-based approaches can efficiently explore and exploit these landscapes.

An example is aerodynamic shape optimization, where traditional methods like genetic algorithms or evolutionary strategies can struggle due to the high computational cost of evaluating each design iteration through simulations. Optimization algorithms can take days because of the computationally expensive bottleneck of traditional simulations.

Here, we introduce the concept of the Surrogate Model. Instead of running expensive simulations for every evaluation, a surrogate model—trained on a limited set of high-fidelity data—provides rapid predictions at a fraction of the cost.

With Machine Learning, surrogate models (e.g., Gaussian processes, neural networks, and 3D Deep Learning models) approximate the objective function, reducing computational cost while guiding optimization toward high-performance designs. The advantage of the Neural Concept platform with 3D Deep Learning is that it minimizes the need for manual simplifications and directly captures complex spatial features, enhancing the optimization process's fidelity.

Examples include using Machine Learning to optimize aerodynamic profiles in aerospace or F1 design, structural topologies in mechanical engineering, thermal management systems in electronics, and manufacturing process parameters in materials science.

In summary, a key technical advantage is that Machine Learning models can serve as efficient surrogate models or metamodels, replacing costly finite element analyses or computational fluid dynamics simulations during optimization. These Machine Learning-driven approaches often combine supervised learning techniques with optimization algorithms to create hybrid solutions that can handle the uncertainty in real-world engineering problems and the constraints typical in engineering design.

How Does Machine Learning Optimization Work? Model Optimization Algorithms

Machine Learning Optimization (or Optimization I, as in the introduction) refers to optimizing the performance of machine learning models. It involves tuning the model’s hyperparameters, selecting appropriate features, choosing the model architecture, and improving the training process to enhance accuracy, reduce overfitting, decrease training time, etc. The goal is to improve the machine learning algorithm’s performance on its task.

Hyperparameters are settings chosen before training a machine learning model, unlike parameters, which the model learns from data. These settings control aspects like model complexity and learning efficiency, influencing performance. Proper tuning of hyperparameters can reduce prediction errors by ensuring the model generalizes well to unseen data. For example, the learning rate in a neural network (NN) determines how much model weights adjust per iteration. A high rate causes instability, while a low rate slows convergence.

Machine Learning Optimization techniques are crucial for making accurate predictions or decisions for training models. Hyperparameter tuning is essential in model optimization. Random searches and grid searches are straightforward approaches to hyperparameter optimization, but they can be computationally expensive. More advanced techniques, such as Bayesian optimization or gradient-based tuning, improve efficiency and performance. These techniques aim to minimize a specific function, often called the loss or cost function.  

Generally, a “cost function” (or objective function) C measures how good or bad a solution is. For example, it might measure a model’s prediction error.

Each method is suited for different scenarios, influenced by the nature of the data, the model’s architecture, and the computational resources available. The choice of optimization method can significantly affect the training speed, the quality of the final model, and its ability to generalize.

Before optimization, data preprocessing—including feature scaling—is crucial to ensure that input parameters contribute proportionally to the optimization process. This step improves the stability of surrogate models like Gaussian Processes and Deep Learning-based approaches, leading to more accurate design predictions

The Gradient Descent Method

Let’s use the gradient descent method to understand the basic mathematics of optimization, which applies to machine learning and engineering problems. Gradient Descent is a first-order iterative algorithm for finding a local minimum of a differentiable multivariate function.

The variable “x” represents what we can control:

• In Machine Learning, x might be model weights (Optimization I)
• In engineering, x might be the shape parameters of a wing (Optimization II)

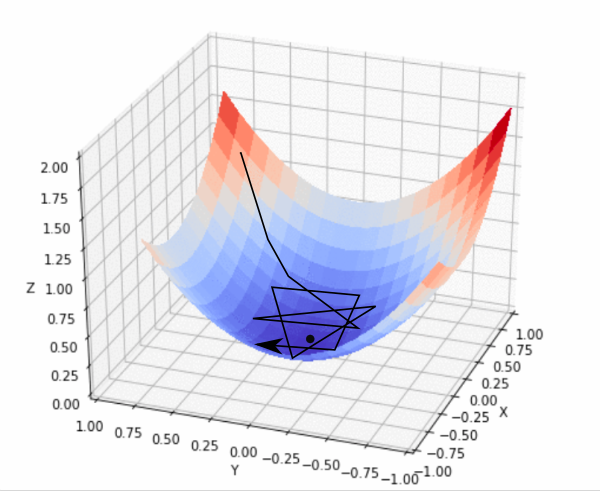
The “loss landscape” is like a terrain map showing how the cost (introduced previously) C varies with x. Imagine hiking in the mountains: Height represents the cost C, our position represents parameters x, and we want to find the lowest point (minimum).

The gradient ∇C indicates the direction in which the function C increases the fastest at our current position. This leads to the gradient descent update rule: Δx = −η∇C, where Δx represents the change in x, η is the learning rate controlling the step size, and the negative sign indicates that we move in the opposite direction of the gradient. This process is repeated iteratively until we converge to a minimum of C. Iterative optimization involves comparing model output with expected results after each iteration.

On the Learning Rate

The learning rate η is a crucial hyperparameter in gradient descent. It controls the step size for each parameter update and determines how aggressively the model moves toward minimizing the cost function C at each iteration.

With a small learning rate (η too low), the machine learning model updates parameters in very small steps, leading to slow convergence. If there is insufficient momentum, it may take excessive iterations to reach the minimum or get stuck in local minima.

With a high learning rate (η too high), the model takes big steps, which can cause it to overshoot the minimum and oscillate without settling. The loss might even diverge in extreme cases of large learning rates, preventing convergence.

Some optimization techniques, like Adam or RMSprop, dynamically adjust the learning rate during training. These methods start with larger steps and refine them as training progresses, balancing speed and stability.

Choosing an optimal learning rate is key to using a training dataset to get the most accurate model. A common strategy is to start with a moderate value of learning rate (e.g., 0.01 for many problems) and decay it over time to fine-tune the solution as the model nears convergence.

Loss Landscape and Gradient Descent

A loss landscape represents how well a machine learning model predicts outcomes across different parameter settings. For example, the difference between the predicted and actual price defines the loss when predicting house prices based on size, bedrooms, and location. This loss is plotted across all possible parameter combinations, forming a multidimensional surface whose height represents the loss value.

The training aims to find the lowest point on this landscape—where loss is minimized. Gradient descent is the optimization method used to navigate this terrain as we saw earlier. The search becomes more complex if the loss landscape has multiple low points (local minima), while a single minimum simplifies optimization. Efficient gradient descent techniques, like momentum or adaptive learning rates, help models converge faster, avoiding poor local minima and ensuring better predictions.

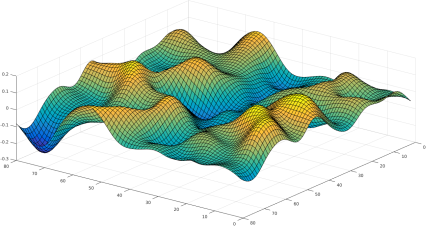
The shape of the loss landscape indicates the model’s behavior and the difficulty of finding minimum loss. A landscape with many local minima may be more challenging to optimize than one with a single global minimum. During optimization, the algorithm updates model parameters using the gradients of the loss function to minimize loss. The iterative process of parameter updates continues until the loss function is minimized or a stopping criterion is met. Thus, descent optimization finds the minimum of the loss function, while the loss landscape visualizes it concerning model parameters.

Stochastic Gradient Descent

Stochastic Gradient Descent is an extension of gradient descent that introduces randomness to speed up convergence and reduce memory usage. Stochastic Gradient Descent computes the gradient and updates model parameters for each training example individually or in small batches.

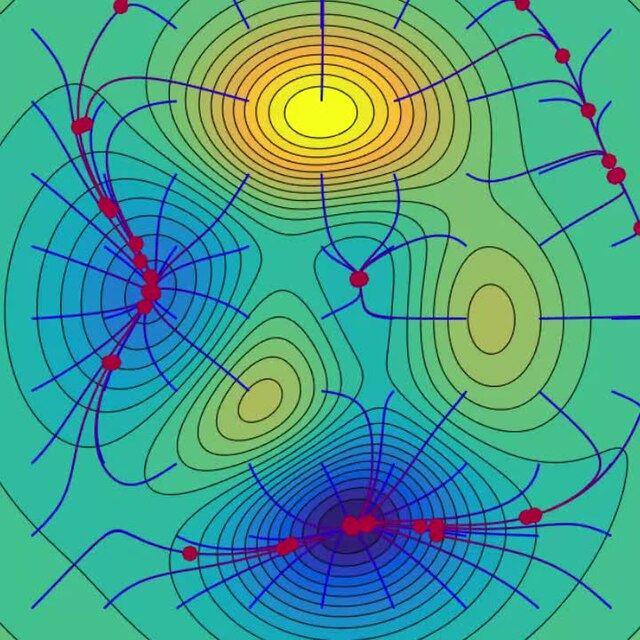
Adaptive Learning Rate Methods

Adagrad adapts the learning rate for each parameter, giving larger updates for infrequent parameters and smaller ones for frequent ones. RMSprop modifies Adagrad by normalizing the gradient using a moving average of squared gradients, preventing the learning rate from decreasing too rapidly.

Objective Functions - ADAM

ADAM (Adaptive Moment Estimation) is a popular optimizer for training deep neural networks. It is particularly effective in high-dimensional, complex loss landscapes. ADAM updates model parameters like gradient descent but adapts the learning rate (η) for each parameter based on historical gradients, improving stability and convergence. Adam is an optimization algorithm that combines ideas from momentum optimization and RMSprop.

Adam is noted for its efficiency in handling sparse gradients, making it suitable for tasks like natural language processing.

Bayesian Optimization

Bayesian optimization provides a rigorous framework for optimizing expensive-to-evaluate objective functions f(x) by maintaining and updating probability distributions over possible solutions. The method constructs a probabilistic surrogate model (typically a Gaussian Process) that captures both the predicted value μ(x) and uncertainty σ(x) at any point x in the search space. Bayesian optimization iteratively improves model performance by refining hyperparameters based on previous results.

Metaheuristic Optimization Algorithms

Metaheuristic optimization algorithms guide lower-level heuristic techniques in optimizing complex search spaces. Many are inspired by natural behaviors, like genetic algorithms mimicking evolution or particle swarm optimization following bird flocking. In evolutionary algorithms, each iteration of a hyperparameter value is assessed and combined with other high-scoring hyperparameter values.

Evolutionary Algorithms: Genetic Algorithms

Genetic algorithms optimize by mimicking natural evolution, using selection to identify solutions. These solutions form a population evaluated by an objective function. The best chromosomes reproduce and generate new solutions through combination and mutation until a satisfactory solution is found. Genetic algorithms can be computationally demanding.

Swarm Intelligence

Swarm intelligence algorithms emulate the collective behavior of organisms to solve optimization problems. The key insight is that simple individual behaviors can create sophisticated collective problem-solving abilities.

Particle Swarm Optimization simulates bird flocking. The core principle is simple: particles adjust their velocities based on their own and their neighbors’ successful experiences. 

Ant Colony Optimization mimics ants finding food through pheromone trails. As more ants choose better paths, these trails strengthen. In the algorithm, virtual ants deposit more pheromones on better solutions, allowing the best paths to accumulate the strongest pheromone levels over time.

The Artificial Bee Colony algorithm mimics how honeybees find nectar. The algorithm uses different types of bees: employed bees stick with known food sources, onlookers choose sources based on their quality, and scouts search for new sources.

How to Create an Optimal Shape: Machine Learning-Based Optimization Examples

Designing industrial objects optimizes shapes for performance, materials, and manufacturability via CAD. For instance, optimizing a car’s rear window for aerodynamics or a lightweight bracket for fatigue resistance requires simulations. CAE simulations assess performance in fluid dynamics or structural analysis, but they may take weeks and demand high computing power.

Companies can enhance CAE by investing in High-Performance Computing (HPC), using GPUs for parallel processing, or, most efficiently, applying AI for real-time simulations.

Deep Neural Networks

Computer-aided engineering (CAE) limits analyses to a few per day due to computational demands, emphasizing the need for real-time alternatives like surrogate models. Deep learning facilitates this through surrogate modeling; techniques such as Neural Concept identify geometric features using NNs. AI and data science are intertwined as AI creates predictive models from consistent datasets like temperature and pressure. NNs minimize prediction errors and link design with performance goals.

Deep learning (DL) relies on data, as training data influences the model’s ability to recognize patterns and make predictions. More data typically enhances performance, but data quality is vital—poor or biased data can undermine results. Unlike traditional AI systems focused on rule-based decisions, DL excels at predictions, leaving final decisions to users, even as optimization capabilities evolve.

The Importance of Training Data

Training data impact model performance, generalization, and accuracy. High-quality, diverse data helps models recognize patterns, reduce bias, and make reliable predictions. In contrast, poor data can result in overfitting, underfitting, or biased outputs, hindering real-world use.

For instance, convolutional neural networks (CNNs) trained on limited medical images may not generalize to new scans, compromising diagnostic reliability. Similarly, self-driving car models trained solely on sunny conditions may struggle in rain or snow. While large datasets enhance performance, when data is lacking, we can implement strategies like synthetic data, transfer learning, and data augmentation.

CNNs are particularly relevant in engineering applications because they can process and analyze complex image-based data. Their strength lies in extracting spatial features from 2D images, 3D models, and CAD designs, making them highly effective for engineering tasks.

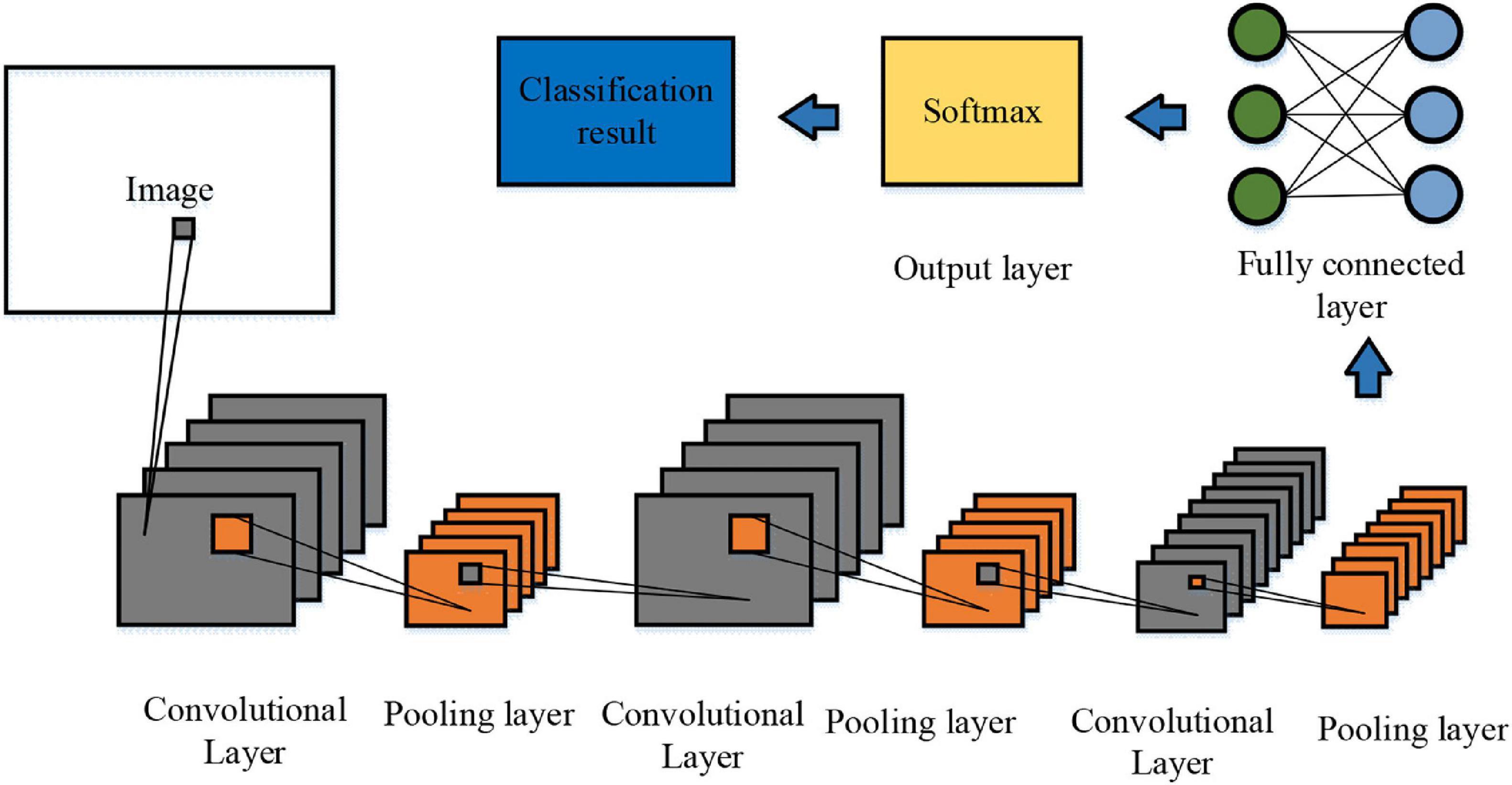
Many believe that deep learning requires millions of samples, but industrial applications like defect detection have succeeded with only a few hundred labeled cases, refining models iteratively. Initial data from past designs can considerably cut future data needs in CAD engineering simulations.

Engineering Optimization

Testing new designs through simulations is time-consuming and costly. Design spaces often have many dimensions, such as material properties and performance metrics, making manual optimization impractical. For example, optimizing a car's aerodynamics involves tuning interrelated parameters like shape and material composition. We need an algorithm to balance objectives—structural strength, weight reduction, and energy efficiency—while considering material and manufacturing cost constraints. The next section will explore efficient industrial design optimization methods.

What Are the Classic Requirements for Optimization Methods?

Optimization theory examines algorithms and strategies for identifying the optimal solution to a problem. Optimization techniques are frequently applied in engineering to develop systems or processes that function efficiently and effectively.

Objective Functions in Deep Learning

In Supervised Learning, the artificial neural networks aim to use known data to minimize a “cost function” C. The C function is the difference between the neural network’s prediction (ŷ) and the actual solution (y) and is also a function of the inputs (x). Therefore, C = C(x;y,ŷ) over the entire dataset. The concept works statistically over a whole dataset composed of samples, each with its own “loss” (i.e., the deviation for a single data point, whereas the cost is for all the data points).

The minimum of this function is the artificial neural networks’ learning solution.

There are several ways to express the cost function mathematically, and a few of them are listed here:

• Mean Absolute Error (MAE) is a loss function used in regression problems by taking the mean of the absolute differences between the predicted and actual values.
• Mean Squared Error (MSE) squares the individual errors instead of calculating their absolute values.
• Root Mean Squared Error (RMSE). RMSE is computed by taking the square root of the MSE.
• R2-score. The R2-score, or R², gives the proportion of the variance in a regression model's response variable that the predictor variables can explain. The higher the R² value, up to a maximum of 1, the better a model fits a dataset.

Cost functions can be managed because supervised learning provides a known solution. Thus, one predictive model can outperform another due to better predictions. This shows the conceptual bridge between learning on one side and achieving optimal designs on the other: both are optimization problems!

Both scenarios involve optimization; supervised learning aims for predictive accuracy, while design optimization seeks the best design based on specific performance objectives and constraints.

How to Optimize a 3D Shape

Starting with a digital product shape in CAD, what algorithmic options assist designers in optimizing functional requirements like weight and mechanical robustness? Standard methods connecting CAD to optimization algorithms include:

1. Topology optimization uses simulations to find optimal material distribution based on constraints like stress and displacement, leading to lightweight designs. However, it is case-specific and inflexible. In contrast, machine learning-based optimization generalizes across design variations by learning patterns.

2. Parametric design allows easy modifications by adjusting parameters and usually meets requirements across different processes or materials. However, it questions whether results are optimal or just improved.

3. Shape optimization offers more flexibility than parametric design, seeking better approximations. It enhances shapes through algorithms, improving performance by reducing drag or increasing stiffness, while allowing free-form deformation without extra constraints.

The idea is now to train the artificial neural network on the AI software to yield, for example, the hydrodynamic coefficients of a wing. The three-dimensional optimization based on machine learning is performed on meshes, whose shape evolves for every iteration until it reaches an “optimal” form for the given constraints.

Applications of Machine Learning-Based Optimization: Case Studies

We will now examine a couple of examples of the use of AI in mechanical engineering, namely, applications of Machine Learning to produce optimal shapes. In such cases, the focus was not on the machine learning model and its hyperparameter optimization, and the collaboration between data scientists and engineers was oriented toward a better-performing industrial design thanks to an accurate Machine Learning / Deep Learning model.

Case Study 1: Heat Exchanger Optimization

Heat exchangers transfer heat between fluids and are prevalent in automotive HVAC systems, enhancing drivers’ comfort. Their designs vary widely and involve complex factors. Due to costly simulations, engineers often iterate on limited design parameters.

The Neural Concept platform showed impressive predictive performance, being able to leverage training data from previous non-optimal designs. The model also analyzed flow in 3D, while the Neural Concept optimization library led to optimized design results. AI predictions were considered as an accurate model of CFD ground truth for temperature and fluid velocity at the heat exchanger’s surface.

Case Study 2: UAV Optimization

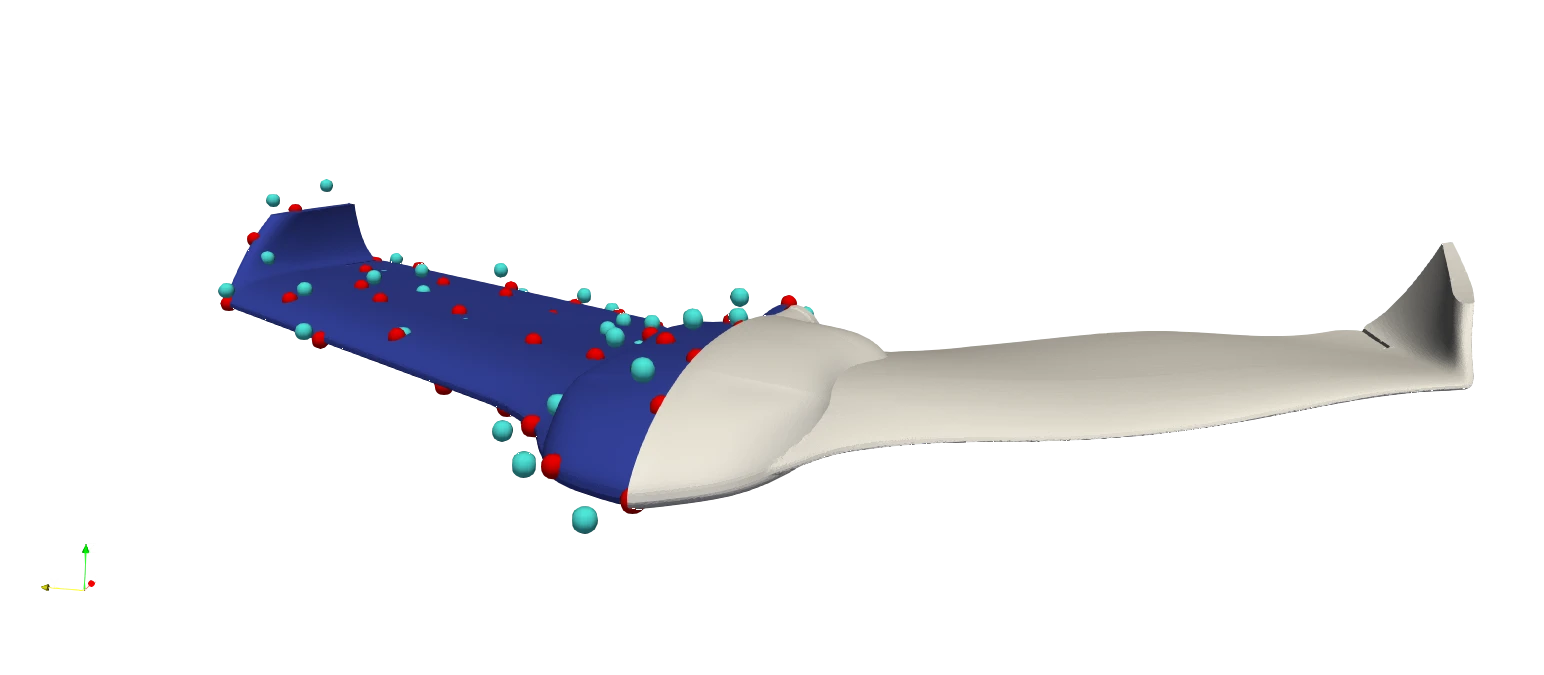
The project sought to meet a UAV’s aerodynamic and geometric requirements while optimizing performance. The algorithm aligned engineering outcomes with actual needs. The optimization process relied on simulation software (CAE) to evaluate UAV performance across configurations, informing design decisions.

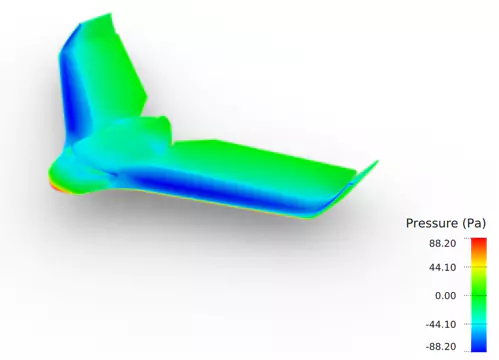
Neural Concept streamlined simulations into AI predictions, exploring and optimizing drone aerodynamics using three CFD simulation levels:

• a rough estimate (“low fidelity”),
• an AirShaper concept simulation,
• a detailed simulation capped at fifty iterations is used to enhance the design.

Low-fidelity CFD and a pre-trained neural network aided in innovative design exploration. The goal was to enhance the lift-to-drag (L/D) ratio crucial for UAV autonomy, and optimization iterations monitored L/D efficiency.

The framework started with low-accuracy simulations for pre-training and refined with high-accuracy simulations.  This approach increased the L/D ratio by 4.25% and reduced drag by 6.25% thus providing an optimal combination.

Future Predictions

Two successful examples highlighted how optimizing a shape may be applied to complicated industrial devices in the automotive and aerospace industries. The presented use cases were a heat exchanger and the entire body of a UAV. For the aerospace and automotive industries, many more external aerodynamics simulation examples show the applicability of Machine Learning to engineers who are not concerned with hyperparameter values and other ML details.

Simulation and optimization software has been on the market for 30+ years. However, using CAE and optimization as decision-making tools has been constrained until now by two factors:

1. The time necessary for execution (hours or days).
2. The specialized knowledge needed (10-20% of engineers are typically competent for simulations).

By offering real-time simulation and democratized custom solutions accessible to all engineers, deep learning simulation and optimization shatter the constraints of conventional methodologies.

As a result, AI is ready to help engineers design faster, better products!

FAQ

Is Supervised Learning similar to design optimization?

Unlike design optimization, which seeks the best solution under constraints, Supervised learning aims to minimize a cost function based on known solutions. However, both are optimization problems that seek optimal outcomes.

What are the challenges associated with optimization in Deep Learning?

High computational demand, risk of overfitting, and navigating complex loss landscapes.

How do optimization algorithms differ between Supervised and Unsupervised Learning?

Supervised uses labeled data for error minimization; Unsupervised focuses on data structure without labels.

What is the role of hyperparameters in Machine Learning models?

Control model behavior, complexity, and learning process, not learned from data.

‍